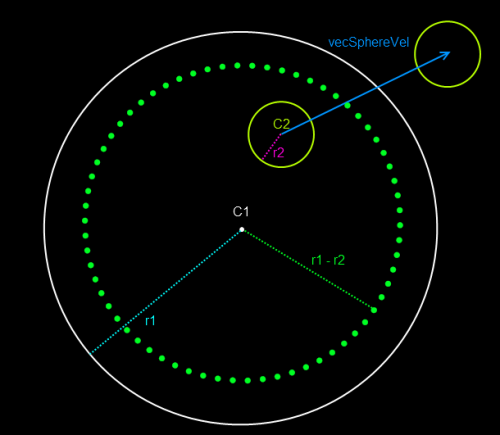
Our previous moving sphere to sphere function works for when the moving sphere starts outside the static sphere sphere, but for when the moving sphere is inside the static sphere, it automatically says there was a collision.
In the case we have a smaller moving sphere starting inside a bigger static sphere and we want to check for when it collides with the containing sphere’s edge, we will need to tweak our algorithm slightly.
First, we’re going to subtract the moving sphere’s radius from the static sphere’s radius, making the containing sphere smaller. If the distance between the containing sphere’s center to the final position of the moving sphere is greater than or equal to this new radius, then there is a collision. Now, we just need to perform a slightly modified ray to sphere test.
If we look at our original ray to sphere function, we ended up with the following formula:
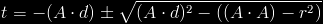
Here, the square root would help us obtain the two points in which the ray hit the sphere. We wanted the first point of contact, so we subtracted the square root from –(A dot d).
In this case, however, we want what would be our “second” point of contact.
The reason is the following:
The ray will still hit the containing sphere two times, the first time it collides with it, however, is at a negative time (i.e. Behind the starting point of the ray), so this value is useless for us. The second time it hits (i.e. The bigger of both roots) is in front of the starting point of the ray, following the ray’s direction.
Here’s a diagram explaining this.
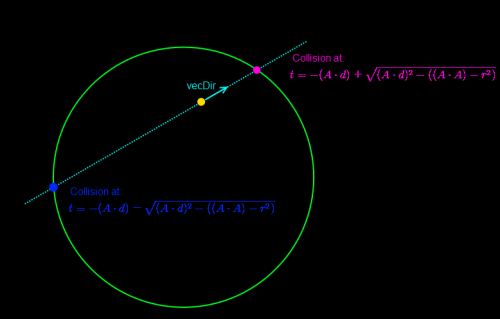
So, we will need to add the square root to –(A dot d) instead of subtracting it. This will give us the time of intersection we’re looking for.
Here’s some sample C++ code that performs this check using the DirectX vector functions.
{
D3DXVECTOR3 m_vecDir;
D3DXVECTOR3 m_vecStart;
};
struct TSphere
{
D3DXVECTOR3 m_vecCenter;
float m_fRadius;
};
bool MovingSphereToContainingSphere(const TSphere& tMovingSphere, const D3DXVECTOR3& vecSphereVel, const TSphere& tStaticSphere, float& fT)
{
//First we check, if the length from the static sphere's center to the final position of the moving sphere
//is not greater or equal to the static sphere's radius minus the moving sphere's radius, then there's no collision.
//We will use squared distances for this.
D3DXVECTOR3 vecToFinalPost((tMovingSphere.m_vecCenter + vecSphereVel) - tStaticSphere.m_vecCenter);
if( D3DXVec3Dot(&vecToFinalPost, &vecToFinalPost) < (tStaticSphere.m_fRadius - tMovingSphere.m_fRadius))
{
return false;
}
//If we get to this point, it means there is a collision!
//First, we subtract the radius of the moving sphere from the static sphere's radius.
//We will save it into a new sphere for ease of use
TSphere tempSphere(tStaticSphere);
tempSphere.m_fRadius -= tMovingSphere.m_fRadius;
//We create a new ray starting at the moving sphere's center with a direction of the
//normalized moving sphere's speed
TRay tempRay;
tempRay.m_vecStart = tMovingSphere.m_vecCenter;
D3DXVec3Normalize(&tempRay.m_vecDir, &vecSphereVel);
//Now, we perform a modified ray to sphere test.
//First, we create a vector from the static sphere's center to the ray's start point
D3DXVECTOR3 vecV1 = tempRay.m_vecStart - tStaticSphere.m_vecCenter;
//Get the dot product of this vector with the ray's direction
//This will become the 'b' part of our quadratic equation
float fB = D3DXVec3Dot(&vecV1, &tempRay.m_vecDir);
//Get the square distance from the start of the ray to the sphere's surface
//This will become the 'c' part of our quadratic equation
float fC = D3DXVec3Dot(&vecV1, &vecV1) - (tempSphere.m_fRadius * tempSphere.m_fRadius);
//We get the discriminant for our equation
float fDisc = fB*fB - fC;
//There's no need to check if the discriminant is negative. The reason is that,
//since the ray starts inside the sphere, it will always collide with it
//We solve our equation and get the time of collision
//We use +sqrt(fDisc) to get the largest root, since the smaller root will be
//an invalid value (negative time)
fT = -fB + sqrt(fDisc);
return true;
}
