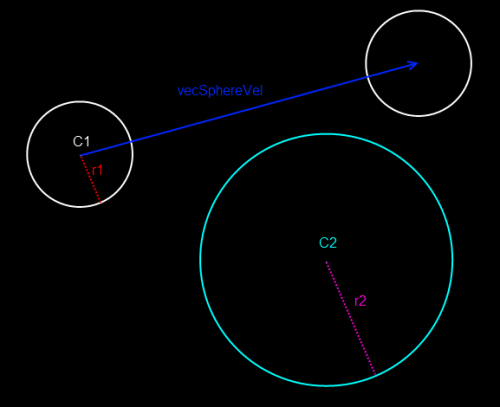
A moving sphere to a static sphere test is basically a slightly modified ray to sphere test.
First, we expand the static sphere’s radius by the moving sphere’s radius. Then, we call our ray to sphere function, sending the normalized velocity vector as the ray’s direction.
Then, we just need to check if the collision point is actually within the boundaries of the line created by the trajectory, so we check if the collision time is less than or equal to the length of the un-normalized velocity vector.
Here’s some sample C++ code to perform this check using the DirectX vector functions. It also contains the code for the ray to sphere test that we need to perform.
struct TRay
{
D3DXVECTOR3 m_vecDir;
D3DXVECTOR3 m_vecStart;
};
struct TSphere
{
D3DXVECTOR3 m_vecCenter;
float m_fRadius;
};
bool MovingSphereToSphere(const TSphere& tMovingSphere, const D3DXVECTOR3& vecSphereVel, const TSphere& tStaticSphere, float& fT)
{
//First, we create a new sphere based on the static sphere's position but with the radius of both spheres
TSphere tempSphere(tStaticSphere);
tempSphere.m_fRadius += tMovingSphere.m_fRadius;
//Now, we get the length of our sphere's velocity. We will use this for the ray to sphere test and to check against collision time
float fVecLength = D3DXVec3Length(&vecSphereVel);
//We create a ray that starts at the moving sphere's center and has a direction of the normalized velocity
TRay tempRay;
tempRay.m_vecStart = tMovingSphere.m_vecCenter;
tempRay.m_vecDir = vecSphereVel / fVecLength;
//We call our ray to sphere function,
if(RayToSphere(tempRay, tempSphere, fT))
{
//We check if the time is less than or equal to the velocity's length
if(fT <= fVecLength)
{
return true;
}
}
return false;
}
bool RayToSphere(const TRay& tRay, const TSphere& tSphere, float &fT)
{
//Create a vector from the sphere to the ray's start point
D3DXVECTOR3 vecV1 = tRay.m_vecStart - tSphere.m_vecCenter;
//Get the dot product of this vector with the ray's direction
//This will become the 'b' part of our quadratic equation
float fB = D3DXVec3Dot(&vecV1, &tRay.m_vecDir);
//Get the square distance from the start of the ray to the sphere's surface
//This will become the 'c' part of our quadratic equation
float fC = D3DXVec3Dot(&vecV1, &vecV1) - (tSphere.m_fRadius * tSphere.m_fRadius);
//If the ray starts outside the sphere and points away from it, we return false
if( fC > 0.0f && fB > 0.0f)
return false;
//Else, we get the discriminant for our equation
float fDisc = fB*fB - fC;
//If this is less than zero, we return false
if( fDisc < 0.0f)
return false;
//If we didn't want the time of collision, we could just return true here.
//But in this case we do want it, so we'll continue
//We solve our equation and get the time of collision
//We use -sqrt(fDisc) to get the smallest root, ie. the first point in which the ray touches the sphere
fT = -fB - sqrt(fDisc);
//If the time is less than zero, it means the ray started inside the sphere
//If so, we just make it zero
if(fT < 0.0f)
fT = 0.0f;
//Our collision point is going to be:
//tRay.m_vecStart + tRay.m_vecDir * fT
return true;
}
{
D3DXVECTOR3 m_vecDir;
D3DXVECTOR3 m_vecStart;
};
struct TSphere
{
D3DXVECTOR3 m_vecCenter;
float m_fRadius;
};
bool MovingSphereToSphere(const TSphere& tMovingSphere, const D3DXVECTOR3& vecSphereVel, const TSphere& tStaticSphere, float& fT)
{
//First, we create a new sphere based on the static sphere's position but with the radius of both spheres
TSphere tempSphere(tStaticSphere);
tempSphere.m_fRadius += tMovingSphere.m_fRadius;
//Now, we get the length of our sphere's velocity. We will use this for the ray to sphere test and to check against collision time
float fVecLength = D3DXVec3Length(&vecSphereVel);
//We create a ray that starts at the moving sphere's center and has a direction of the normalized velocity
TRay tempRay;
tempRay.m_vecStart = tMovingSphere.m_vecCenter;
tempRay.m_vecDir = vecSphereVel / fVecLength;
//We call our ray to sphere function,
if(RayToSphere(tempRay, tempSphere, fT))
{
//We check if the time is less than or equal to the velocity's length
if(fT <= fVecLength)
{
return true;
}
}
return false;
}
bool RayToSphere(const TRay& tRay, const TSphere& tSphere, float &fT)
{
//Create a vector from the sphere to the ray's start point
D3DXVECTOR3 vecV1 = tRay.m_vecStart - tSphere.m_vecCenter;
//Get the dot product of this vector with the ray's direction
//This will become the 'b' part of our quadratic equation
float fB = D3DXVec3Dot(&vecV1, &tRay.m_vecDir);
//Get the square distance from the start of the ray to the sphere's surface
//This will become the 'c' part of our quadratic equation
float fC = D3DXVec3Dot(&vecV1, &vecV1) - (tSphere.m_fRadius * tSphere.m_fRadius);
//If the ray starts outside the sphere and points away from it, we return false
if( fC > 0.0f && fB > 0.0f)
return false;
//Else, we get the discriminant for our equation
float fDisc = fB*fB - fC;
//If this is less than zero, we return false
if( fDisc < 0.0f)
return false;
//If we didn't want the time of collision, we could just return true here.
//But in this case we do want it, so we'll continue
//We solve our equation and get the time of collision
//We use -sqrt(fDisc) to get the smallest root, ie. the first point in which the ray touches the sphere
fT = -fB - sqrt(fDisc);
//If the time is less than zero, it means the ray started inside the sphere
//If so, we just make it zero
if(fT < 0.0f)
fT = 0.0f;
//Our collision point is going to be:
//tRay.m_vecStart + tRay.m_vecDir * fT
return true;
}
24 / Jun 2010
