In our previous ray to sphere test, we just checked if the ray collided with the sphere.
Sometimes, however, we need to check the time value in which this collision happens.
The test is similar, however, some things need to be added.
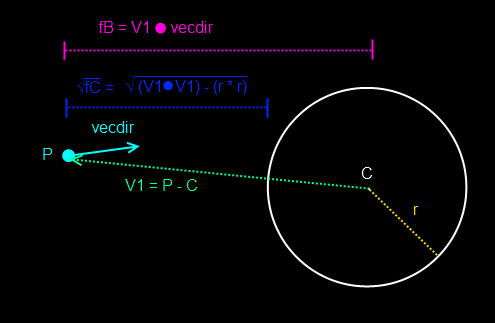
The distance between a point ‘P’ on the very edge of the sphere to the center of the sphere would be equals to the radius of the sphere. So, if we make a vector from the center of the sphere to this point, it would be P – C.
If we calculate the dot product of P – C with itself, we will get its squared length, which is equals to the squared radius.
(P – C) dot (P – C) = r * r
We can simplify this by having a variable A = P – C
A dot A = r*r
If we then add the ray’s direction ‘d’ multiplied by a time value ‘t’, we get
(A + t * d) dot (A + t * d) = r * r
We can transform this into an equation:
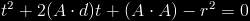
This is a quadratic equation, since ‘t’ is the value we want to obtain, we can just use the usual solution for quadratic formulas. After simplifying, we end up with this:
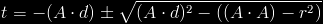
What is inside the square root is called the “discriminant”. If this is a negative value, we can immediately know that the ray doesn’t touch the sphere.
We get two values, depending if we use the positive square root or the negative. These two roots represent the two points in which the ray crosses the sphere. If they are equal, it means the ray only touches the sphere at one point. We only want the first point in which the sphere is touched, so we need the smallest root, so, we’ll use the negative one.
If, after solving this, we get a negative time, it means the ray started inside the sphere, so we can clamp it to zero.
We could call our point in sphere function if we know that having a ray starting inside a sphere is going to be a common case.
To get our collision point, we just multiply the direction of the ray by the collision time and add it to the ray’s start point.
Here’s some sample C++ code to perform this collision check using the DirectX vector functions.
{
D3DXVECTOR3 m_vecDir;
D3DXVECTOR3 m_vecStart;
};
struct TSphere
{
D3DXVECTOR3 m_vecCenter;
float m_fRadius;
};
bool RayToSphere(const TRay& tRay, const TSphere& tSphere, float &fT)
{
//Create a vector from the sphere to the ray's start point
D3DXVECTOR3 vecV1 = tRay.m_vecStart - tSphere.m_vecCenter;
//Get the dot product of this vector with the ray's direction
//This will become the 'b' part of our quadratic equation
float fB = D3DXVec3Dot(&vecV1, &tRay.m_vecDir);
//Get the square distance from the start of the ray to the sphere's surface
//This will become the 'c' part of our quadratic equation
float fC = D3DXVec3Dot(&vecV1, &vecV1) - (tSphere.m_fRadius * tSphere.m_fRadius);
//If the ray starts outside the sphere and points away from it, we return false
if( fC > 0.0f && fB > 0.0f)
return false;
//Else, we get the discriminant for our equation
float fDisc = fB*fB - fC;
//If this is less than zero, we return false
if( fDisc < 0.0f)
return false;
//If we didn't want the time of collision, we could just return true here.
//But in this case we do want it, so we'll continue
//We solve our equation and get the time of collision
//We use -sqrt(fDisc) to get the smallest root, ie. the first point in which the ray touches the sphere
fT = -fB - sqrt(fDisc);
//If the time is less than zero, it means the ray started inside the sphere
//If so, we just make it zero
if(fT < 0.0f)
fT = 0.0f;
//Our collision point is going to be:
//tRay.m_vecStart + tRay.m_vecDir * fT
return true;
}
