This test can be used for when testing the collision between a ray or a line segment against a sphere.
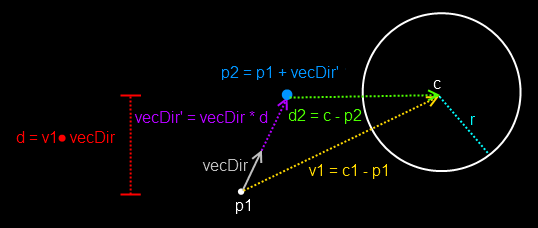
First, we need the direction of the ray. If we were checking against a line segment, we will then just use the normalized vector from the beginning of the line segment to the end.
We create a new vector from the ray’s beginning point to the center of the sphere, and we get the projection of this vector onto the ray’s direction. This is obtained by doing the dot product of this vector with the ray’s direction vector.
If the result of this dot product is less than zero, it means the ray is pointing away from the sphere and hence we won’t have a collision.
The next part of the test is a point in sphere test. The point we will need to use for this calculation is the closest point to the sphere. To get this point, we will need to scale the ray’s direction vector by the dot product we just calculated and add it to the ray’s start point.
Then, we just call our point in sphere function with this new point.
Here’s some sample code in C++ that performs the ray to sphere collision check (it also includes the point in sphere function at the bottom).
{
D3DXVECTOR3 m_vecDir;
D3DXVECTOR3 m_vecStart;
};
struct TSphere
{
D3DXVECTOR3 m_vecCenter;
float m_fRadius;
};
bool RayToSphere(const TRay& tRay, const TSphere& tSphere)
{
//First, let's see if the point is inside the sphere. If so, return true
if(PointInSphere(tSphere, tRay.m_vecStart))
return true;
//Create a vector from the ray's start to the sphere's center
D3DXVECTOR3 vecV1(tSphere.m_vecCenter - tRay.m_vecStart);
//Project this vector onto the ray's direction vector
float fD = D3DXVec3Dot(&vecV1, &tRay.m_vecDir);
//If the ray is pointing away
if(fD < 0.0f)
return false;
//Calculate the closest point to the sphere
D3DXVECTOR3 vecClosestPoint(tRay.m_vecStart + ( tRay.m_vecDir * fD ));
//Check if that point is inside the sphere
return (PointInSphere(tSphere, vecClosestPoint));
}
//Point in sphere function:
bool PointInSphere(const TSphere& tSph, const D3DXVECTOR3& vecPoint)
{
//Calculate the squared distance from the point to the center of the sphere
D3DXVECTOR3 vecDist(tSph.m_vecCenter - vecPoint);
float fDistSq( D3DXVec3Dot( &vecDist, &vecDist) );
//Calculate if the squared distance between the sphere's center and the point
//is less than the squared radius of the sphere
if( fDistSq < (tSph.m_fRadius * tSph.m_fRadius))
{
return true;
}
//If not, return false
return false;
}
