Collisions between spheres are very simple and easy to perform.
An advantage that spheres have over things like AABBs (Axis-Aligned Bounding Boxes) is that it doesn’t matter if the object rotates, the sphere will remain the same.
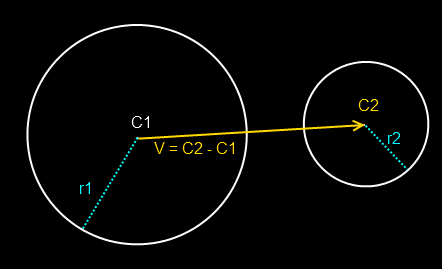
We need to calculate the distance between the centers of the spheres and compare it to the sum of their radii. If this distance is less than the sum of their radii, then the spheres are overlapping. If it’s the same, then the spheres are just touching.
To get the distance between the centers of the sphere, we need to create a vector between their centers.
We then calculate the length of that vector against the sum of the radii.
However, a more efficient way to do this would be the following:
The dot product of a vector with itself equals the squared length of that vector. So, we can just calculate the squared length of out vector against the square of the sum of the radii, that way we don’t need to calculate the length of the vector, which is an expensive operation!
Here’s some sample C++ code you can use to calculate sphere to sphere collisions with the DirectX Vector functions.
{
D3DXVECTOR3 m_vecCenter;
float m_fRadius;
};
bool SphereToSphere(const TSphere& tSph1, const TSphere& tSph2)
{
//Calculate the squared distance between the centers of both spheres
D3DXVECTOR3 vecDist(tSph2.m_vecCenter - tSph1.m_vecCenter);
float fDistSq( D3DXVec3Dot( &vecDist, &vecDist) );
//Calculate the squared sum of both radii
float fRadiiSumSquared( tSph1.m_fRadius + tSph2.m_fRadius );
fRadiiSumSquared *= fRadiiSumSquared;
//Check for collision
//If the distance squared is less than or equal to the square sum
//of the radii, then we have a collision
if( fDistSq <= fRadiiSumSquared )
return true;
//If not, then return false
return false;
}
