The half-space test allows us to see the position of a point respective to a plane. We can determine if this point is in front of the plane, behind the plane or on the plane.
This is a very useful test, as it is used in many types of collision detection functions, especially when testing against triangles.
Depending on whether or not we have a point on the plane we’re testing against, the half space test can be performed in a couple of different ways.
First case – We have a point on the plane:
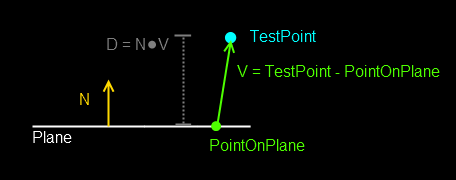
We create a vector from the point on the plane to the point we’re testing against.
We get the dot product of the plane’s normal with this new vector. This is the distance between the plane to the test point.
If the distance is positive, the point is in front of the plane.
If the distance is negative, the point is behind the plane.
If the distance is zero, it means the point is on the plane.
(NOTE: In this example, instead of zero we will check against an EPSILON value. This way, avoiding possible floating point errors. This is also called making a “thick plane”)
Here’s some sample C++ code for this case using the DirectX Vector functions.
//This can be replaced with just a bool, depending on how the special case (point on plane) wants to be handled
short HalfSpaceTest(const D3DXVECTOR3& vecTestPoint, const D3DXVECTOR3& vecNormal, const D3DXVECTOR3& vecPointOnPlane)
{
//Calculate a vector from the point on the plane to our test point
D3DXVECTOR3 vecTemp(vecTestPoint - vecPointOnPlane);
//Calculate the distance: dot product of the new vector with the plane's normal
float fDist(D3DXVec3Dot(&vecTemp, &vecNormal));
if(fDist > EPSILON)
{
//Point is in front of the plane
return 0;
}
else if(fDist < -EPSILON)
{
//Point is behind the plane
return 1;
}
//If neither of these were true, then the point is on the plane
return 2;
}
Second case – We don’t have a point on the plane:
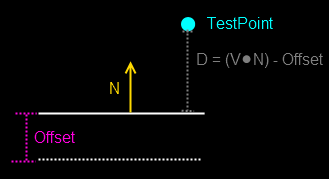
When we don’t have a point on the plane, we usually have an offset value.
The distance of the test point to the plane will be calculated by getting the dot product of the plane’s normal with the test point and then subtracting the offset value.
If the distance is positive, the point is in front of the plane.
If the distance is negative, the point is behind the plane.
If the distance is zero, it means the point is on the plane.
(NOTE: In this example, instead of zero we will check against an EPSILON value. This way, avoiding possible floating point errors. This is also called making a “thick plane”)
Here’s some sample C++ code for this case using the DirectX Vector functions.
//This can be replaced with just a bool, depending on how the special case (point on plane) wants to be handled
short HalfSpaceTest(const D3DXVECTOR3& vecTestPoint, const D3DXVECTOR3& vecNormal, float fOffset)
{
//Calculate the distance: dot product of the new vector with the plane's normal minus the offset
float fDist(D3DXVec3Dot(&vecTestPoint, &vecNormal) - fOffset);
if(fDist > EPSILON)
{
//Point is in front of the plane
return 0;
}
else if(fDist < -EPSILON)
{
//Point is behind the plane
return 1;
}
//If neither of these were true, then the point is on the plane
return 2;
}
