Intro:
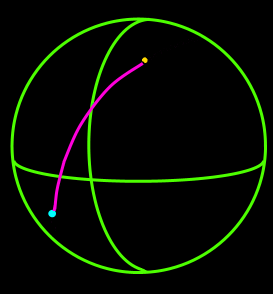
The main part of the project I’m currently working on is about traveling around little planets. For some calculations, we needed to know the distance between two objects standing on the planet, so, we had to do some research on how to find the spherical distance between two points.
The “great-circle distance” formula required latitudes and longitudes and contained square roots, divisions, and many trigonometric functions, which are not really something we want to do in real time simulation. So, I came up with a solution using the things we already had in our game: matrices.
Approaching the problem from a 2D perspective:
We needed to calculate the shortest distance between these two objects. We can’t have a straight line since we are on a sphere, however, we can create a curved line between both points. If we somehow kept drawing this curved line, always keeping the same distance from the center of the sphere, we will end up drawing a circle.
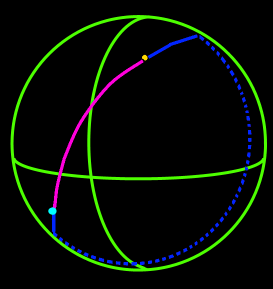
When we look at the problem this way, we can see that the curved line between both points can be represented as a fraction of the circumference, which we already know is :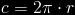 
Now, the only thing we need to do is calculate this amount.
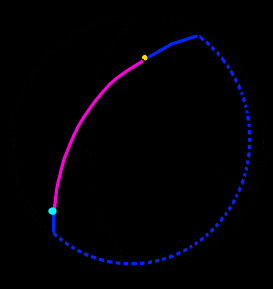
Calculations:
The formula of a circumference is 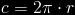because a whole circle (360 degrees) is equal to 2*pi radians and then we just multiply by the radius of the sphere. So, what we need to calculate is the angle between the two points and then multiply that by the radius of the sphere and we will get the amount of the circumference between both points, which is effectively the distance between them.
This is where we use our matrices: each object has its own matrix, which means each object has its own X, Y and Z axes. In case we didn’t have any matrices, the Y axis can be obtained by getting the normalized vector from the center of the sphere to the point/object’s position. We need to normalize the Y axis of both objects (in the case of our project, they are already normalized, so we don’t need to perform that slow operation), get the arc-cosine of the dot product between them and then multiply the result by the radius of the sphere.
(Sample code after the image)
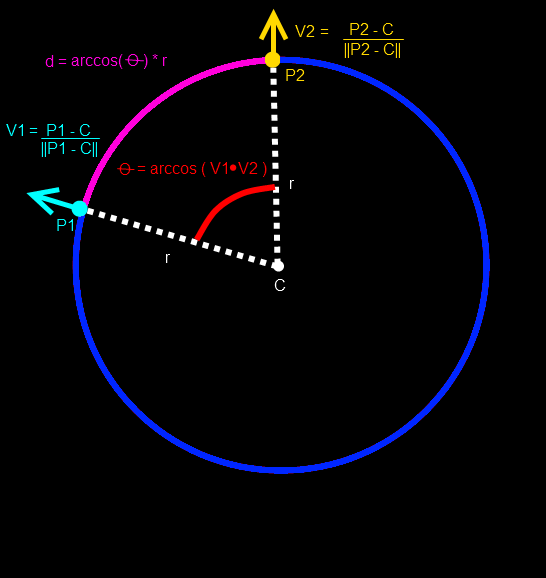
Here’s some sample code in C++ using a generic Matrix class, to avoid depending on whether the matrix is row major or column major.
{
//First, we store the Y axis of both objects
CVector3 tempY1(obj1.GetYAxis()), tempY2(obj2.GetYAxis());
//This is just a robustness check, in case we plan on using this with objects
//whose matrices that are not normalized
if(!tempY1.IsNormalized())
tempY1.Normalize();
if(!tempY2.IsNormalized())
tempY2.Normalize();
//This is the formula, we'll use a generic dot product function for this example
return acos(Vec3Dot(tempY1, tempY2)) * GetRadius();
}